혼공학습단의 완주를 2024년 시작의 목표로 잡았던 날이 엊그제 같은데 벌써 2월이네요... 시간은 정말 빠릅니다.
이번 주에는 오랜만에 여유를 되찾았습니다. 그런데 늦잠이라는 요 녀석이 안와야 할 때는 오더니만 와도 될 때는 안 오는... 참 청개구리 같은 녀석입니다.🐸🐸
뭐 암튼 2월에도 다들 열심히 공부하고 보람차게, 보내보자구요!!
Ch 06-1. 군집 알고리즘
✔️ 비지도 학습(unsupervised learning)
: 타깃이 없을 때 사용하는 머신러닝 알고리즘
✔️ 실습
1) 데이터 준비
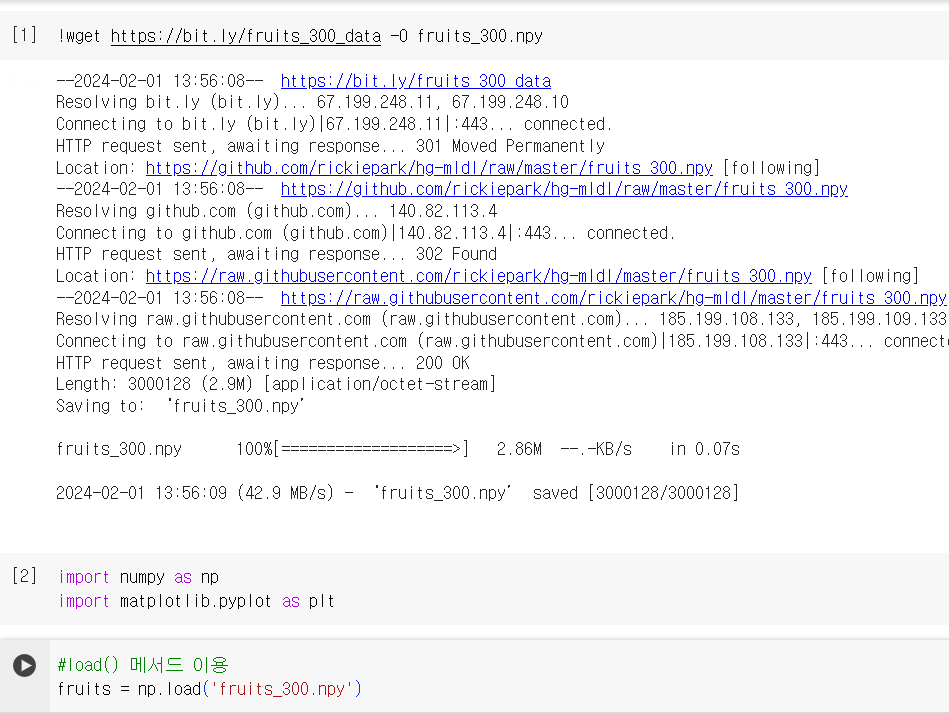
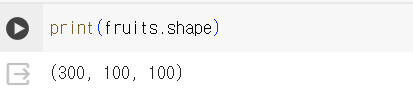
- imshow(): 넘파이 배열로 저장된 이미지를 그릴 수 있음. matplotlib 내장 함수
- 흑백 이미지 → cmap 매개변수를 'gray'로 지정
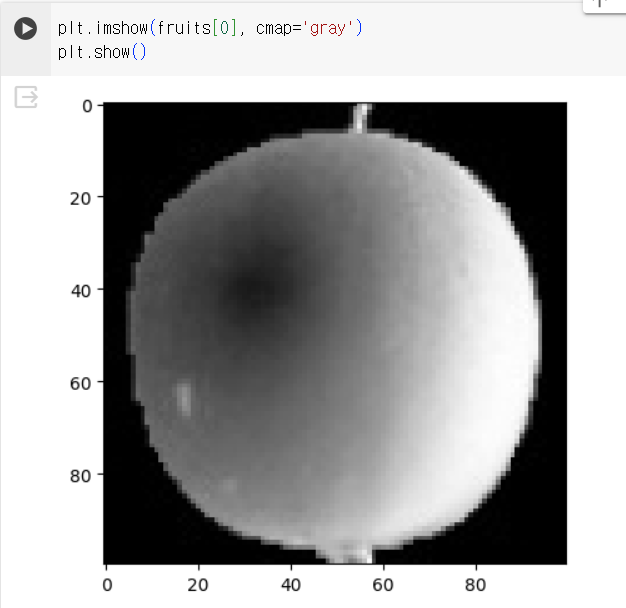
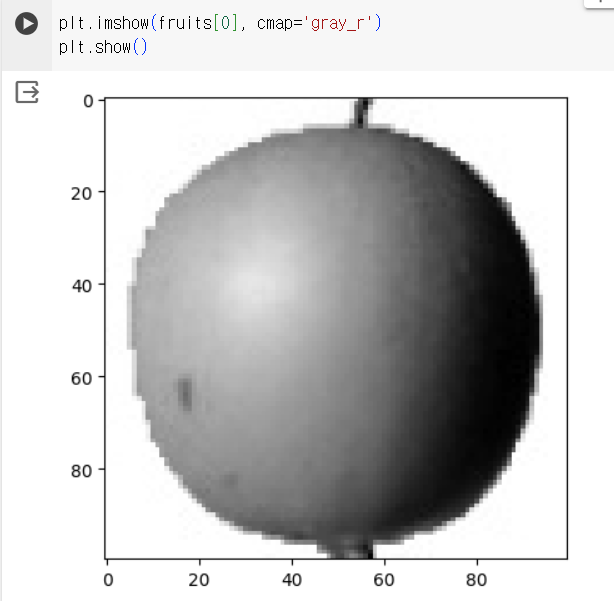
⇒ 관심 대상에 집중하기 위해 배경과 대상을 반전시킴(=배경을 검게 만들고 대상을 밝은색으로 만듦)
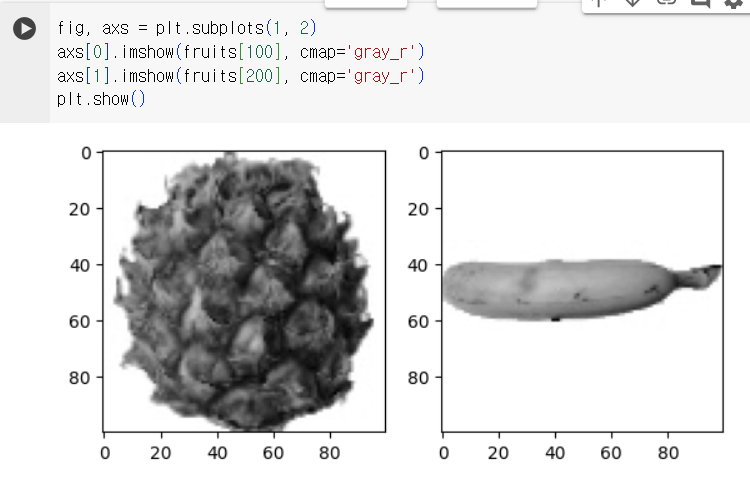
2) 픽셀값 분석하기
- 100 ×100을 10000 ×1로 변환( ∵배열의 편리성 ↑)

- 배열에 들어있는 샘플의 픽셀 평균값 계산
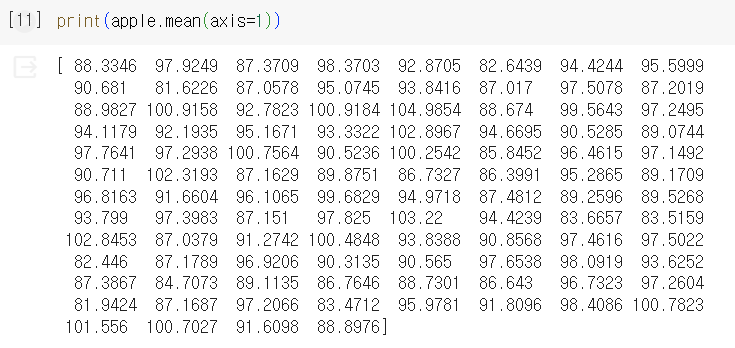
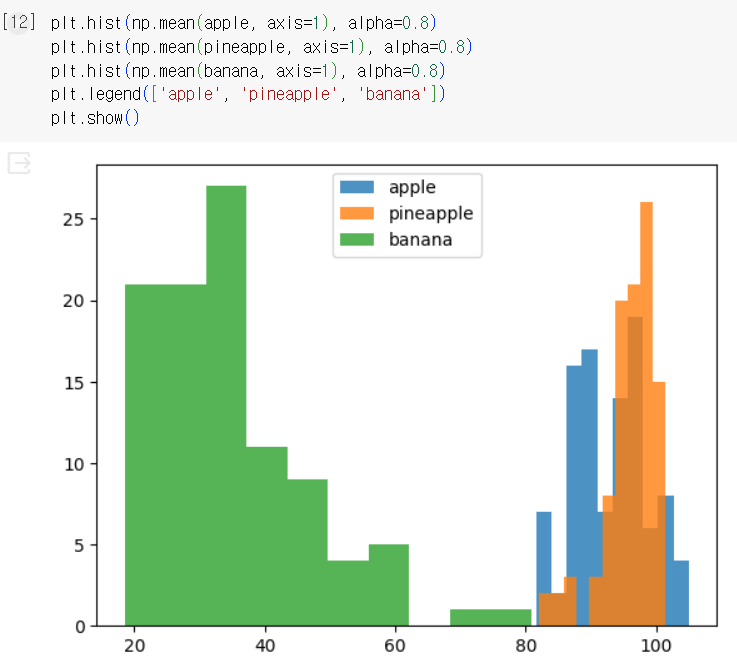
- 픽셀별 평균값 계산 (axis=0)
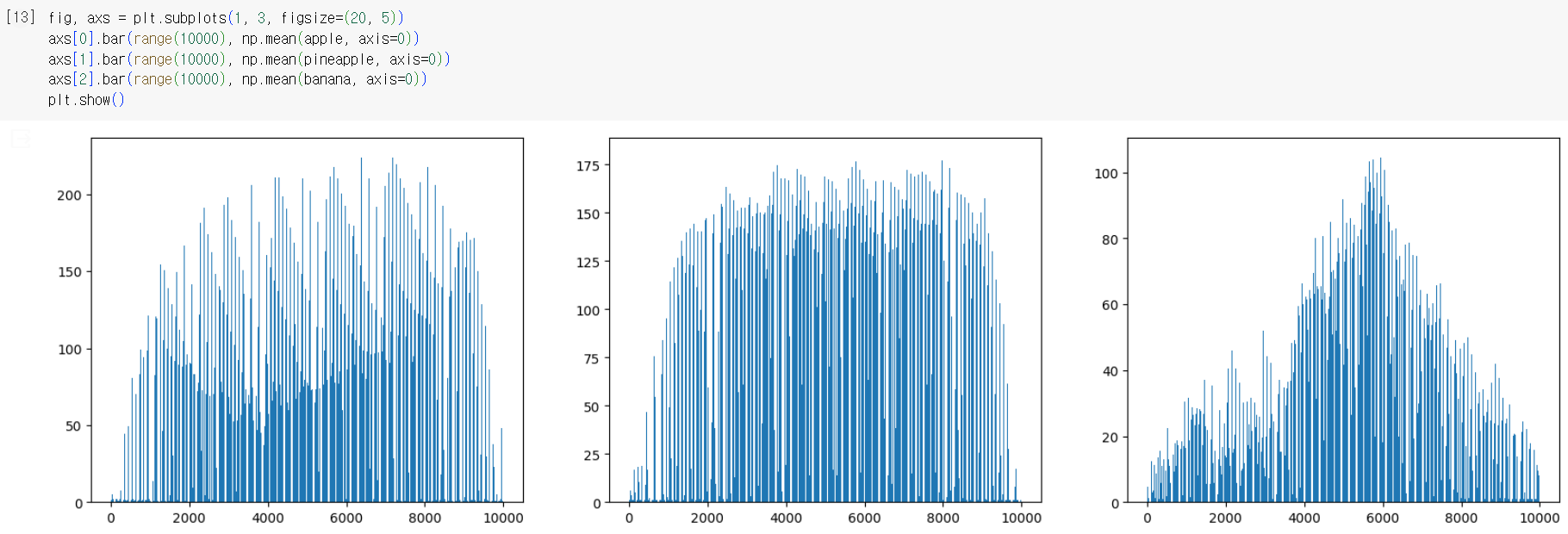

3) 평균값과 가까운 사진 고르기
- 절댓값 오차 이용
- abs(): 절댓값을 계산. 넘파이 내장 함수. absolute()와 동일

- argsort(): 작은 것에서 큰 순서대로 나열한 배열의 인덱스 반환


- 군집(clustering): 비슷한 샘플끼리 그룹으로 모으는 작업. 대표적인 비지도 학습 작업
- 클러스터(cluster): 군집 알고리즘에서 만든 그룹
Ch 06-2. k-평균
✔️ k-평균(k-means) 알고리즘
- cluster center(=centroid): 평균값이 클러스터의 중심에 위치한다는 말에서 유래
- 작동방식
- 무작위로 k개의 클러스터 중심을 정함
- 각 샘플에서 가장 가까운 중심을 찾아 해당 클러스터의 샘플로 지정
- 클러스터에 속한 샘플의 평균값으로 클러스터 중심을 변경
- 클러스터 중심에 변화가 없을 때까지 2번으로 돌아가 반복
- 최적의 k 찾기
- 엘보우 방법
: 클러스터 개수를 늘려가면서 이너셔의 변화를 관찰하여 최적의 클러스터 개수를 찾는 방법
클러스터 개수를 증가시키면서 이너셔를 그래프로 그리면 감소하는 속도가 꺾이는 지점: 클러스터 개수를 늘려도 이너셔가 크게 줄어들지 X
cf. 이너셔: 클러스터 중심과 클러스터에 속한 샘플 사이의 거리 제곱의 합
- 실습
inertia_: 자동으로 이너셔를 계산
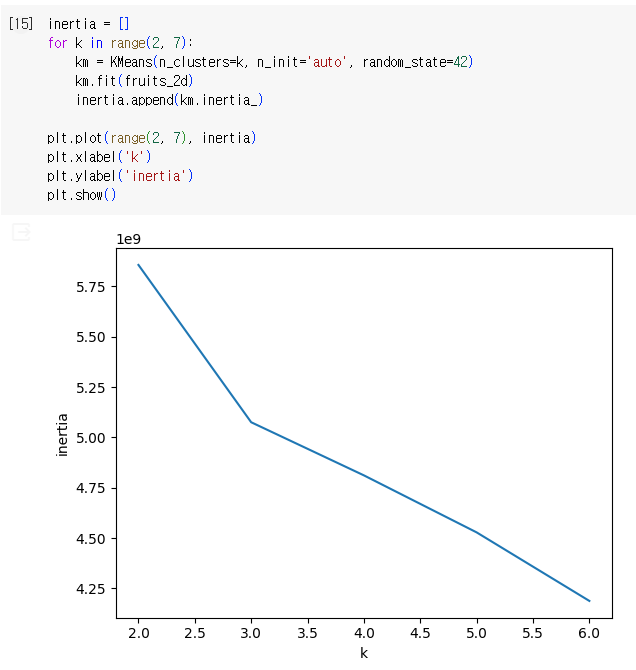
✔️ 실습
1) 데이터 준비
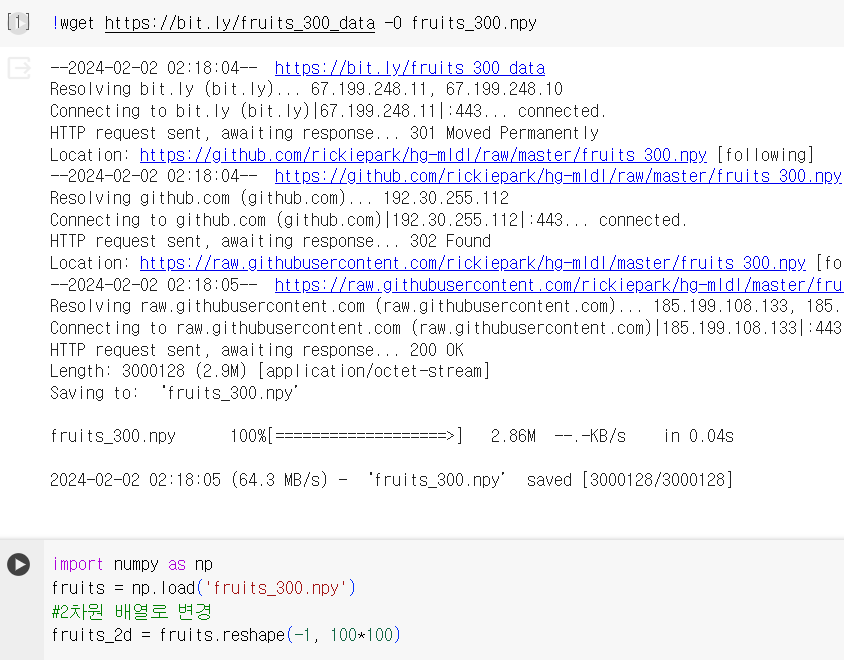
2) 데이터 학습: k-means 사용
- n_cluster: 클러스터 개수 지정

3) 결과 확인









- k-means가 찾은 클러스터 중심을 이미지로 출력

- transform(): 훈련 데이터 샘플에서 클러스터 중심까지 거리로 변환

- predict(): 가장 가까운 클러스터 중심을 예측 클래스로 출력


Ch 06-3. 주성분 분석
✔️ 차원과 차원 축소
- 차원: 데이터가 가진 속성
- 차원 축소: 비지도 학습 작업 중 하나로, 데이터를 가장 잘 나타내는 일부 특성을 선택하여 데이터 크기를 줄이고 지도학습 모델의 성능 향상에 기여
(+) 원본차원으로 손실을 최대한 줄이면서 복원 가능 ex) 주성분 분석(principal component analysis = PCA)
✔️ 주성분 분석(PCA)
: 데이터에 있는 분산이 큰 방향을 찾는 것
- 주성분의 특징
- 원본 차원과 같음
- 주성분으로 바꾼 데이터는 차원이 줄어듦
- 일반적으로 주성분은 원본 특성의 개수만큼 찾을 수 있음
✔️ 실습
1) 데이터 준비
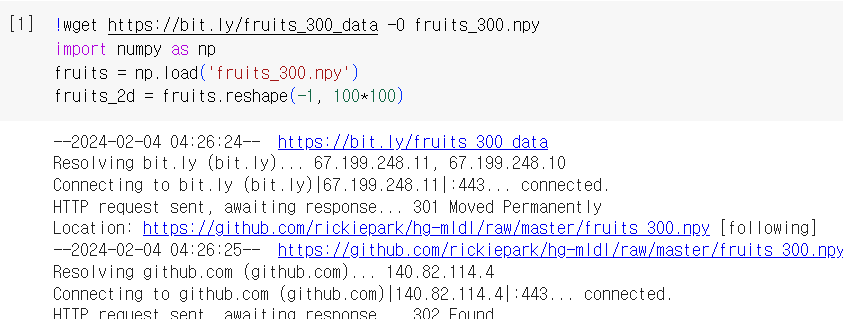
2) 주성분 분석 알고리즘 사용
- n_components 매개변수에 주성분의 개수 지정
- fit() 매서드에 타깃값 제공 X ( ∵ 비지도 학습)


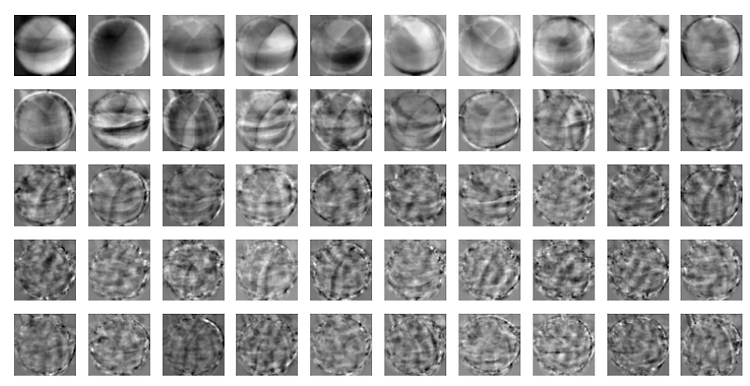
3) 주성분을 그림으로 나타내기(06-2 실습 참고)
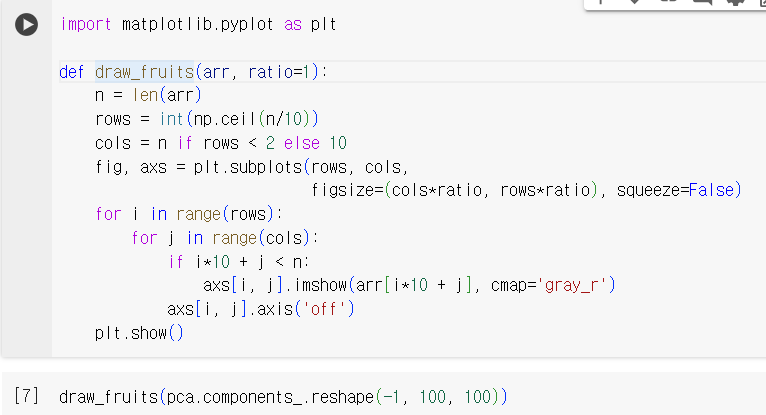
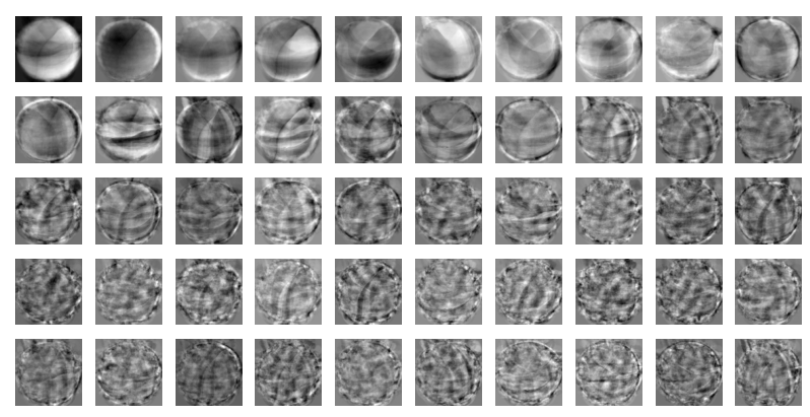
4) transform()을 이용해 원본 데이터의 차원 변환

🍎 원본 데이터 재구성
1) 축소한 특성 복원

2) 100 ×100으로 바꾸어 100개씩 출력




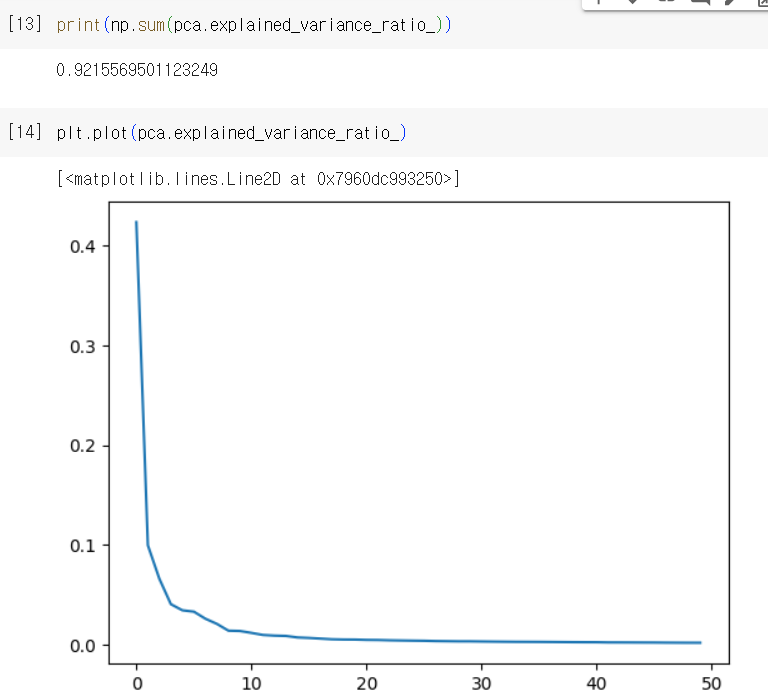
✔️ 설명된 분산(explained variance)
: 주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값
- explained_variance_ratio_에 저장
- 첫 번째 주성분의 설명된 분산이 가장 큼
- 분산 비율을 모두 더하면 50개의 주성분으로 표현하고 있는 총 분산 비율을 얻을 수 있음
✔️ 다른 알고리즘과 함께 사용하기(feat. 로지스틱 회귀 모델)
🍎 과일 사진 원본 데이터 vs. PCA로 축소한 데이터
1) 로지스틱 회귀 모델 및 타깃값 생성

2-1) 원본 데이터 바탕으로 교차 검증

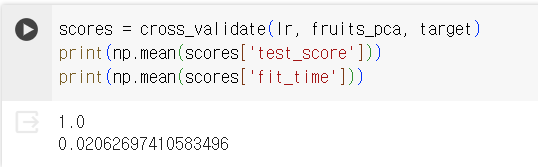
2-2) PCA 데이터 바탕으로 교차 검증
✅ 06-3 확인문제
Q. 특성이 20개인 대량의 데이터셋이 있다. 이 데이터셋에서 찾을 수 있는 주성분 개수는?
A. 20개. 일반적으로 특성의 개수만큼 주성분 개수를 찾을 수 있음
Q. 샘플 개수가 1,000개이고 특성 개수는 100개인 데이터셋이 있다. 즉, 이 데이터셋의 크기는 (1000, 100)이다. 이 데이터를 사이킷런의 PCA 클래스를 이용해 10개의 주성분을 찾아 변환했다. 변환된 데이터셋의 크기는?
A. (1000, 10). 샘플의 개수는 그대로이고, 특성 개수만 100에서 10으로 바뀜
Q. 위의 문제에서 설명된 분산이 가장 큰 주성분은 몇 번째인가?
A. 첫 번째 주성분 (블로그 내용 참고)
'Activities > [혼공단 11기] 머신러닝+딥러닝' 카테고리의 다른 글
| 6주차_Ch.07 딥러닝을 시작합니다 (0) | 2024.02.15 |
|---|---|
| 4주차_Ch.05 트리 알고리즘 (3) | 2024.01.28 |
| 3주차_Ch.04 다양한 분류 알고리즘 (5) | 2024.01.21 |
| 2주차_ Ch.03 회귀 알고리즘과 모델 규제 (1) | 2024.01.14 |
| 1주차_Ch.02 데이터 다루기 (2) | 2024.01.02 |

혼공학습단의 완주를 2024년 시작의 목표로 잡았던 날이 엊그제 같은데 벌써 2월이네요... 시간은 정말 빠릅니다.
이번 주에는 오랜만에 여유를 되찾았습니다. 그런데 늦잠이라는 요 녀석이 안와야 할 때는 오더니만 와도 될 때는 안 오는... 참 청개구리 같은 녀석입니다.🐸🐸
뭐 암튼 2월에도 다들 열심히 공부하고 보람차게, 보내보자구요!!
Ch 06-1. 군집 알고리즘
✔️ 비지도 학습(unsupervised learning)
: 타깃이 없을 때 사용하는 머신러닝 알고리즘
✔️ 실습
1) 데이터 준비

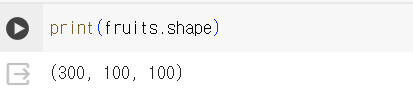
- imshow(): 넘파이 배열로 저장된 이미지를 그릴 수 있음. matplotlib 내장 함수
- 흑백 이미지 → cmap 매개변수를 'gray'로 지정

⇒ 관심 대상에 집중하기 위해 배경과 대상을 반전시킴(=배경을 검게 만들고 대상을 밝은색으로 만듦)


2) 픽셀값 분석하기
- 100 ×100을 10000 ×1로 변환( ∵배열의 편리성 ↑)

- 배열에 들어있는 샘플의 픽셀 평균값 계산


- 픽셀별 평균값 계산 (axis=0)


3) 평균값과 가까운 사진 고르기
- 절댓값 오차 이용
- abs(): 절댓값을 계산. 넘파이 내장 함수. absolute()와 동일

- argsort(): 작은 것에서 큰 순서대로 나열한 배열의 인덱스 반환


- 군집(clustering): 비슷한 샘플끼리 그룹으로 모으는 작업. 대표적인 비지도 학습 작업
- 클러스터(cluster): 군집 알고리즘에서 만든 그룹
Ch 06-2. k-평균
✔️ k-평균(k-means) 알고리즘
- cluster center(=centroid): 평균값이 클러스터의 중심에 위치한다는 말에서 유래
- 작동방식
- 무작위로 k개의 클러스터 중심을 정함
- 각 샘플에서 가장 가까운 중심을 찾아 해당 클러스터의 샘플로 지정
- 클러스터에 속한 샘플의 평균값으로 클러스터 중심을 변경
- 클러스터 중심에 변화가 없을 때까지 2번으로 돌아가 반복
- 최적의 k 찾기
- 엘보우 방법
: 클러스터 개수를 늘려가면서 이너셔의 변화를 관찰하여 최적의 클러스터 개수를 찾는 방법
클러스터 개수를 증가시키면서 이너셔를 그래프로 그리면 감소하는 속도가 꺾이는 지점: 클러스터 개수를 늘려도 이너셔가 크게 줄어들지 X
cf. 이너셔: 클러스터 중심과 클러스터에 속한 샘플 사이의 거리 제곱의 합
- 실습
inertia_: 자동으로 이너셔를 계산

✔️ 실습
1) 데이터 준비

2) 데이터 학습: k-means 사용
- n_cluster: 클러스터 개수 지정

3) 결과 확인









- k-means가 찾은 클러스터 중심을 이미지로 출력

- transform(): 훈련 데이터 샘플에서 클러스터 중심까지 거리로 변환

- predict(): 가장 가까운 클러스터 중심을 예측 클래스로 출력


Ch 06-3. 주성분 분석
✔️ 차원과 차원 축소
- 차원: 데이터가 가진 속성
- 차원 축소: 비지도 학습 작업 중 하나로, 데이터를 가장 잘 나타내는 일부 특성을 선택하여 데이터 크기를 줄이고 지도학습 모델의 성능 향상에 기여
(+) 원본차원으로 손실을 최대한 줄이면서 복원 가능 ex) 주성분 분석(principal component analysis = PCA)
✔️ 주성분 분석(PCA)
: 데이터에 있는 분산이 큰 방향을 찾는 것
- 주성분의 특징
- 원본 차원과 같음
- 주성분으로 바꾼 데이터는 차원이 줄어듦
- 일반적으로 주성분은 원본 특성의 개수만큼 찾을 수 있음
✔️ 실습
1) 데이터 준비

2) 주성분 분석 알고리즘 사용
- n_components 매개변수에 주성분의 개수 지정
- fit() 매서드에 타깃값 제공 X ( ∵ 비지도 학습)


3) 주성분을 그림으로 나타내기(06-2 실습 참고)


4) transform()을 이용해 원본 데이터의 차원 변환

🍎 원본 데이터 재구성
1) 축소한 특성 복원

2) 100 ×100으로 바꾸어 100개씩 출력




✔️ 설명된 분산(explained variance)
: 주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값
- explained_variance_ratio_에 저장
- 첫 번째 주성분의 설명된 분산이 가장 큼
- 분산 비율을 모두 더하면 50개의 주성분으로 표현하고 있는 총 분산 비율을 얻을 수 있음

✔️ 다른 알고리즘과 함께 사용하기(feat. 로지스틱 회귀 모델)
🍎 과일 사진 원본 데이터 vs. PCA로 축소한 데이터
1) 로지스틱 회귀 모델 및 타깃값 생성

2-1) 원본 데이터 바탕으로 교차 검증

2-2) PCA 데이터 바탕으로 교차 검증

✅ 06-3 확인문제
Q. 특성이 20개인 대량의 데이터셋이 있다. 이 데이터셋에서 찾을 수 있는 주성분 개수는?
A. 20개. 일반적으로 특성의 개수만큼 주성분 개수를 찾을 수 있음
Q. 샘플 개수가 1,000개이고 특성 개수는 100개인 데이터셋이 있다. 즉, 이 데이터셋의 크기는 (1000, 100)이다. 이 데이터를 사이킷런의 PCA 클래스를 이용해 10개의 주성분을 찾아 변환했다. 변환된 데이터셋의 크기는?
A. (1000, 10). 샘플의 개수는 그대로이고, 특성 개수만 100에서 10으로 바뀜
Q. 위의 문제에서 설명된 분산이 가장 큰 주성분은 몇 번째인가?
A. 첫 번째 주성분 (블로그 내용 참고)
'Activities > [혼공단 11기] 머신러닝+딥러닝' 카테고리의 다른 글
| 6주차_Ch.07 딥러닝을 시작합니다 (0) | 2024.02.15 |
|---|---|
| 4주차_Ch.05 트리 알고리즘 (3) | 2024.01.28 |
| 3주차_Ch.04 다양한 분류 알고리즘 (5) | 2024.01.21 |
| 2주차_ Ch.03 회귀 알고리즘과 모델 규제 (1) | 2024.01.14 |
| 1주차_Ch.02 데이터 다루기 (2) | 2024.01.02 |